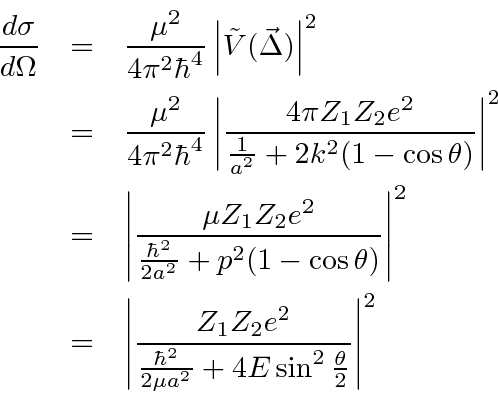Rutherford Scattering Cross Section

Let θ be the deflection angle corresponding to an impact parameter of b.

Rutherford scattering cross section. It corresponds well with the experiment rutherford did in which particles were scattered from atoms in a foil. Plugging in the previously derived expression for the impact parameter b θ we find the rutherford differential scattering cross section d σ d ω z 1 z 2 e 2 8 π ϵ 0 m v 0 2 2 csc 4 θ 2. The scattering process can be treated statistically in terms of the cross section for interaction with a nucleus which is considered to be a point charge ze.

If the scattering target is in the form of a thin foil of thickness l x 10 m. With density gm cm3 the scattered fraction for angles greater than degrees. The differential cross section dσ dθ with respect to the scattering angle is the number of scatterings between θand θ dθ per unit flux per unit range of angle i e.

The cross section σ for an impact parameter b is the area of a circle with radius b. If we scatter from a bare charge where there is no screening we can take the limit in which. The scattering cross 3.

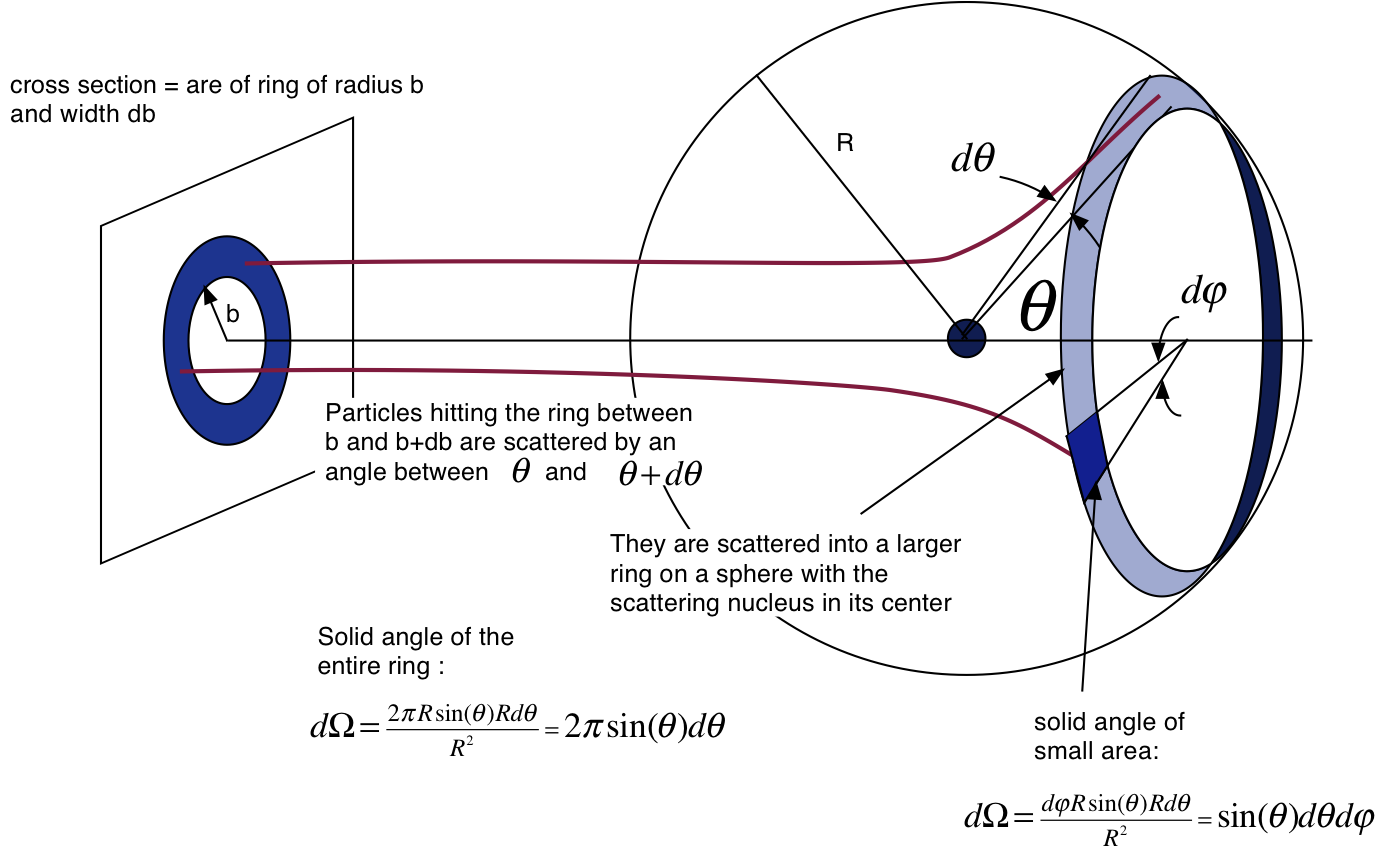
The scattering cross section is fm2 barns. If is the probability per unit time of the particle being scattered into the range of solid angle to then the differential scattering cross section is defined via reif 1965. To see how this notion is useful to us let s imagine that instead of one target we have devised an experiment which in fact contains many targets as shown in figure 3.

Dσ dθ dn θ fdθ π d2 4 cos θ 2 sin 3 θ 2. His formula is in terms of the cross section for an interaction. For example the rutherford cross section is a measure of probability that an alpha particle will be deflected by a given angle during a collision with an atomic nucleus cross section is typically denoted σ and is expressed in terms of the transverse area that the.

It is more usual to quote the differential cross section with respect to a given solid angle. Rutherford scattering cross section consider a particle of type incident with relative velocity onto an ensemble of particles of type with number density. Is expected to be x10.